CS180 Project 6: Neural Radiance Fields (NeRF)

Kenny Wang
SID: 3037341680

UC Berkeley

Overview

In this project, we train a neural radiance field representation for this cute little lego tracked loader.

Part 1: Fitting a Neural Field to a 2D Image

We can use a Neural Radiance Field (NeRF) to represent a 3D scene, but let's start by practicing on a 2D example. We can train a Neural Field to represent a 2D image, predicting R, G, B values from x, y coordinates.

Here is the neural network architecture we will use, a 4-layer multi-layer perceptron (MLP) architecture.

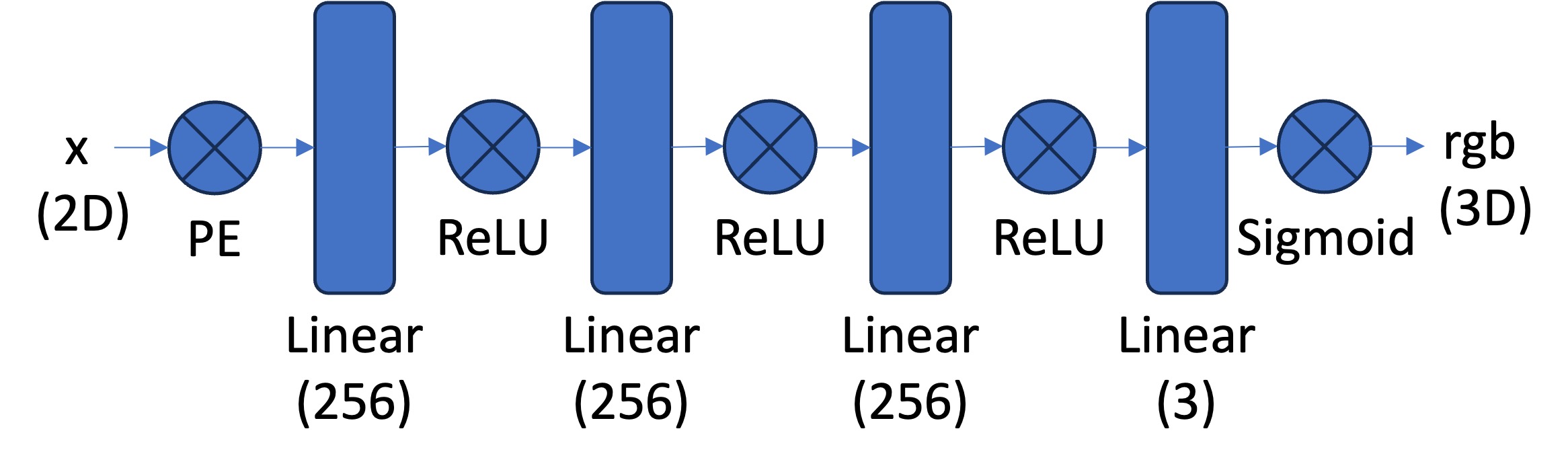
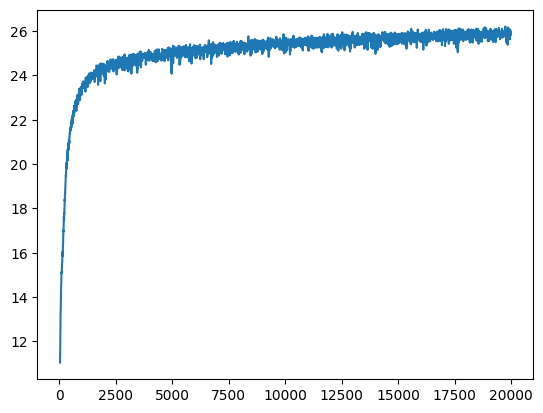
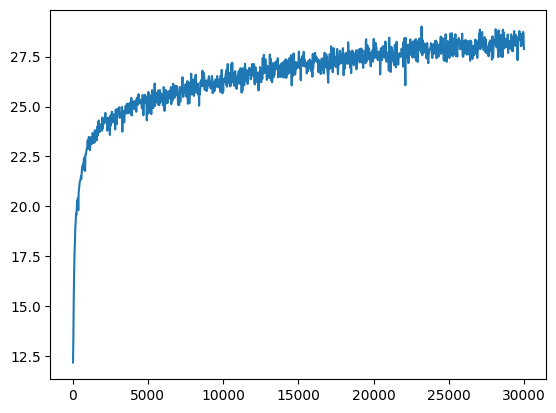
To sample for each batch/epoch, we will randomly select 10,000 points (with replacement, just to make the code faster/simpler) from the image. We're using the Adam optimizer with lr=1e-2, and MSE loss. Training until 20k epochs only takes about 1 minute!

100 epochs

500 epochs

20k epochs

Original

Here's the PSNR curve.

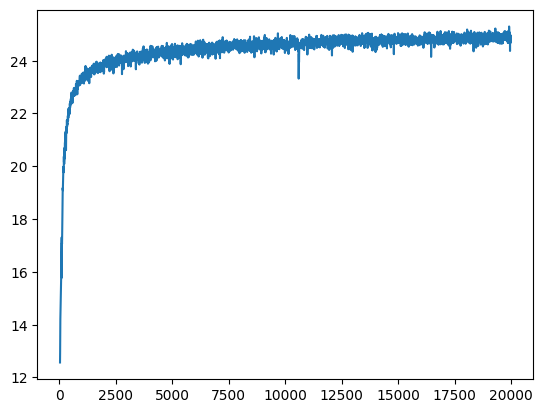
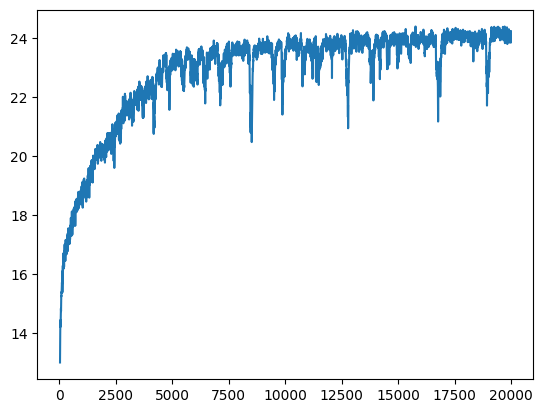
We can try messing with the hyperparameters too. Here's two examples. One is using L=5 instead of 10 for the positional encoding, which we can see is worse. Another is using lr=1e-3 instead of lr=1e-2, which is actually ... better than the standard params!!

L=5

Standard Params

lr=1e-3

Original

Here's the PSNR curves for comparison.

L=5

Standard Params

lr=1e-3

Let's try on another image.

100 epochs

500 epochs

20k epochs

Original

Part 2: Fitting a Neural Radiance Field from Multi-view Images

2.1: Creating Rays from Cameras

Before we can train our model, we can create some useful helper functions first.

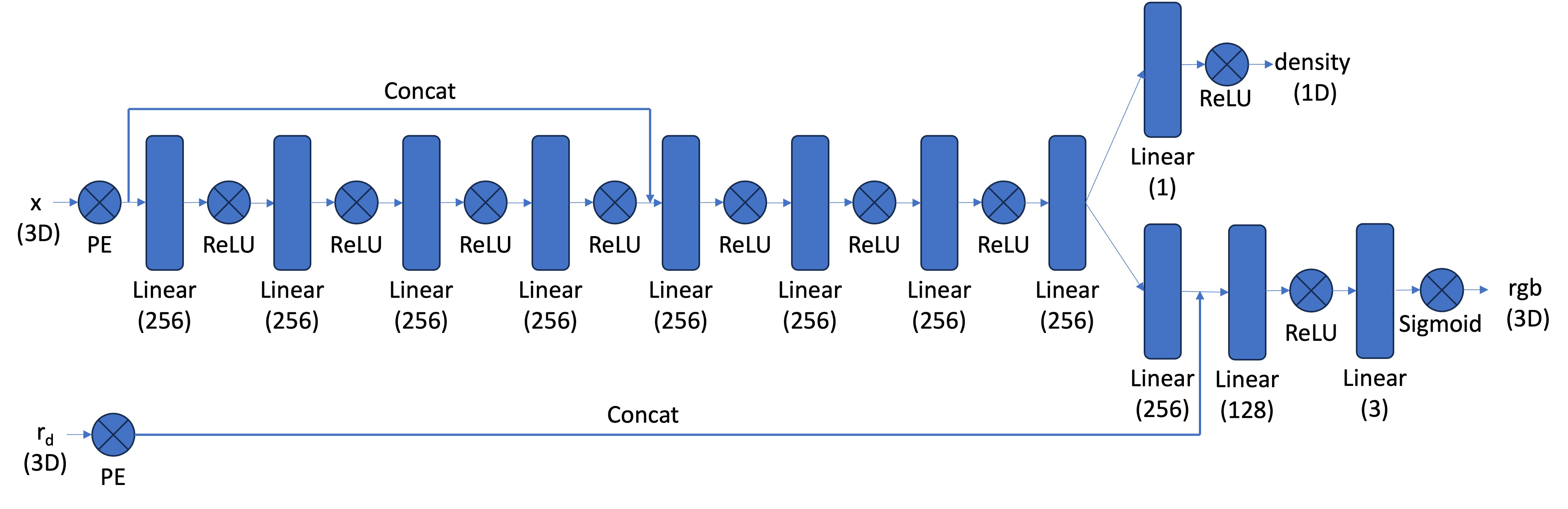
Camera to World Coordinate Conversion. First, we implement x_w = transform(c2w, x_c), which takes in batched 3D camera coordinates x_c and a 4x4 camera-to-world matrix c2w and outputs batched 3D world coordinates. This is a straightforward matrix multiplication, but internally, the function also converts to and from homogeneous coordinates.

Pixel to Camera Coordinate Conversion. x_c = pixel_to_camera(K, uv, s) takes in 3x3 intrinsic matrix K, batched 2D (u,v) pixel coordinates uv, and depth scalar s. It outputs the batched pixel coordinates converted into 3D camera coordinates. This involves just a bit of linear algebra.

Pixel to Ray. ray_o, ray_d = pixel_to_ray(K, c2w, uv) converts pixel (u,v) coordinates into the origin and direction of their associated 3D ray. The function takes in 3x3 intrinsic matrix K, batched 4x4 camera-to-world matrices c2w, and batched 2D (u,v) pixel coordinates uv. It outputs ray_o, the 3D origin vector, and ray_d, the 3D direction vector of the ray.

2.2: Sampling

Sampling Rays from Images. I implemented a RaysData class to act as a dataloader, taking as parameters the intrinsic matrix K, a collection of images imgs, and the corresponding 4x4 camera-to-world matrices c2ws. It stores all the pixels in its set of images into one long flattened array, and has the method sample_rays. This method randomly selects batch_size pixels from the entire set of images, returning ray_o and ray_d, representing the rays for each of those pixels, and rgb, the RGB pixel values. This sampling function uses the helper functions we created earlier.

Sampling Points along Rays. To sample points along rays, I implemented the function sample_along_rays, which takes in ray_o and ray_d to represent a batch of rays. It then outputs the 3D coordinates of 64 points along each ray between distances 2.0 and 6.0. The optional perturb parameter determines whether to add slight randomness to the otherwise evenly-spaced points, and is useful for training.

2.3: Dataloading

Using the visualization code, we can see an example of how rays and points would be sampled for one iteration of training our neural network. However, since we train using 10,000 rays at a time, I'll just show 100 of them.

2.4: Neural Radiance Field

Now it's time to actually create our neural network. We will use a pretty big multi-layer perceptron network, much deeper than the 2D example. Note that this model takes in both 3d coordinates and the ray direction, and it needs to predict both RGB and density values.

For training, we'll use the Adam optimizer with lr=5e-4.

2.5: Volume Rendering

The last step before training the model is to set up volume rendering. The volume rendering equation is: \[\begin{align} C(\mathbf{r})=\int_{t_n}^{t_f} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) d t, \text { where } T(t)=\exp \left(-\int_{t_n}^t \sigma(\mathbf{r}(s)) d s\right) \end{align}\] But we'll use the discrete approximation: \[\begin{align} \hat{C}(\mathbf{r})=\sum_{i=1}^N T_i\left(1-\exp \left (-\sigma_i \delta_i\right)\right) \mathbf{c}_i, \text { where } T_i=\exp \left(-\sum_{j=1}^{i-1} \sigma_j \delta_j\right) \end{align}\] where \(\textbf{c}_i\) is the RGB color output from our network at sample location \(i\), \(T_i\) is the probability of the ray not terminating before sample location \(i\), and \(1 - e^{-\sigma_i \delta_i}\) is the probability of terminating at sample location \(i\).

Following this equation, we now write the function volrend(sigmas, rgbs, step_size) which takes in batched densities sigmas, batched RGB pixel values rgbs, and the distance between points in the ray step_size. The function outputs the final observed RGB pixel value.

Putting it All Together

After getting some initial results, I decided to train the model to 30,000 iterations overnight on my laptop. Here we can visualize the results of our model at different stages of training. Training for the full amount of time really helped nail down the small details, like the studs and holes in the lego pieces.

100 epochs

200 epochs

500 epochs

1k epochs

10k epochs

30k epochs

1k epochs (< 20 minutes)

30k epochs (~9 hours)

Here's the PSNR curve for training to 30k epochs.

Changing Background Color

To change the background color from black to something else, we just need to slightly modify the volume rendering equation by adding one weighted extra term at the end for the background color. First, let's try with the less-trained model (1k iterations).

Using this with the highly-trained model (30k iterations) actually reveals what I'm pretty sure is a black table that the model is resting on!

Reflection

Possibly the second most challenging solo project I've ever done, after the diffusion project. Debugging tensor dimensions was an enormous pain, and the nature of neural networks makes debugging not so straightforward. However, I gained even more familiarity with PyTorch and learned more about ML.

Acknowledgements

This project is a course project for CS 180. Website template is used with permission from Bill Zheng in the Fall 2023 iteration of the class.